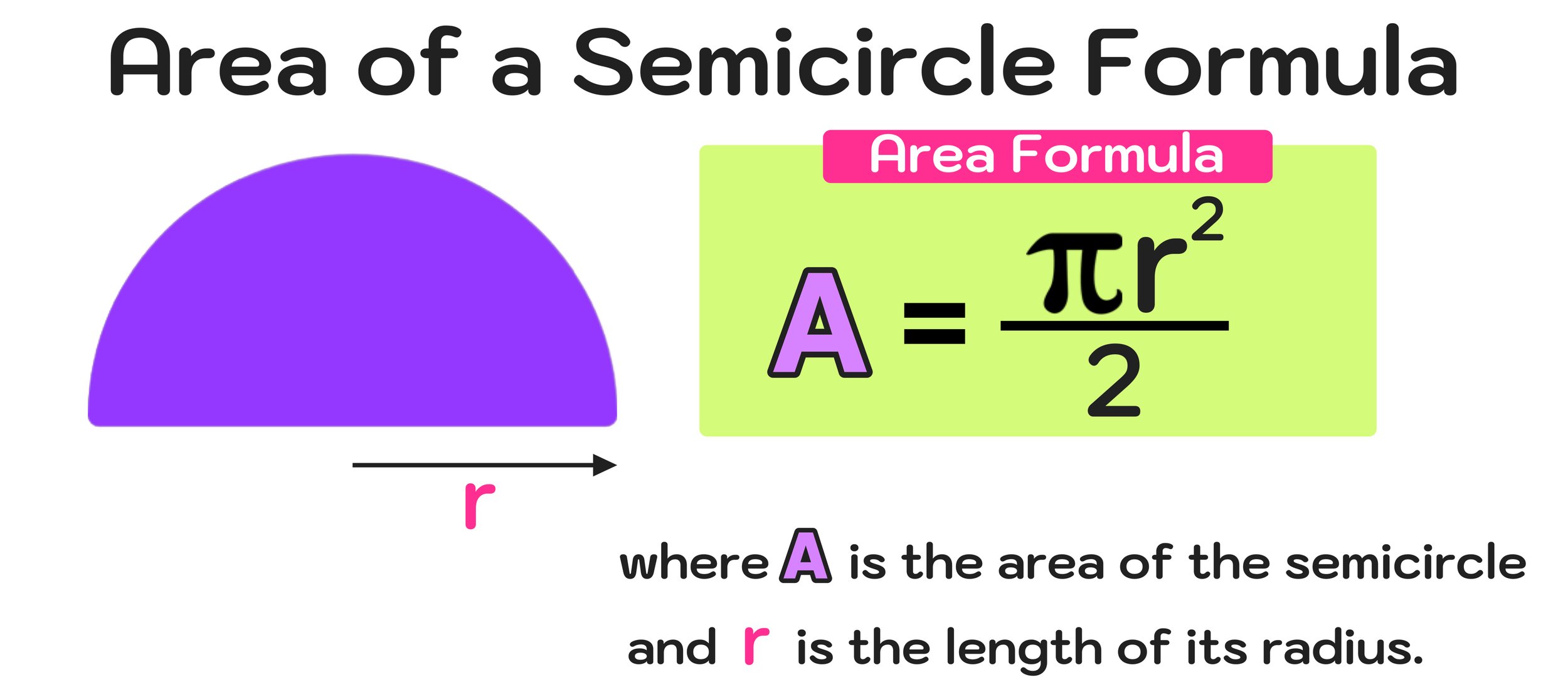
The semicircle area formula is one of the most essential concepts in geometry, widely used in fields like mathematics, engineering, architecture, and even design. Whether you're a student trying to ace your exams or a professional working on complex geometrical projects, understanding this formula is a must. This simple yet powerful mathematical tool helps us calculate the area of a semicircle—half of a full circle—making it invaluable when dealing with partial circular shapes.
But why is the semicircle area formula so significant? Its applications go far beyond the classroom or textbook problems. From determining the space occupied by a curved structure to calculating the cross-sectional area of a pipe, the semicircle area formula is everywhere around us. By mastering this concept, you'll unlock countless practical applications that can simplify your work and make your calculations faster and more accurate.
In this comprehensive guide, we'll dive deep into the semicircle area formula, breaking it down step by step. We'll explore its derivation, real-world applications, and even tackle common questions to ensure you have a thorough understanding of the topic. So, let's roll up our sleeves and get started on this journey to mastering the semicircle area formula!
Read also:West Coast Earthquake Impacts Preparedness And Future Predictions
Table of Contents
- What Is a Semicircle?
- Why Do We Need the Semicircle Area Formula?
- How to Derive the Semicircle Area Formula?
- Step-by-Step Guide to Calculating Semicircle Area
- Semicircle Area Formula with Real-Life Examples
- What Are the Key Variables in the Formula?
- Common Mistakes When Using the Semicircle Area Formula?
- Semicircle Area in Geometry and Trigonometry
- Applications of the Semicircle Area Formula
- How Does the Formula Compare to Other Shapes?
- Semicircle Area vs. Full Circle Area
- Frequently Asked Questions
- Examples of Semicircle Area in Architecture
- Conclusion
What Is a Semicircle?
A semicircle is, simply put, half of a circle. If you were to take a full circle and cut it along its diameter, you would end up with two equal semicircles. These shapes are characterized by their curved edge (the arc) and the straight edge (the diameter). Semicircles are widely used in both theoretical and practical contexts, from architectural designs to mathematical problems.
In mathematical terms, a semicircle is defined as the set of all points that lie on one-half of a circle and are bounded by the diameter. This makes the semicircle a two-dimensional geometric figure with its own unique properties and formulas, including the semicircle area formula, which we will explore in detail.
Why Do We Need the Semicircle Area Formula?
Understanding the semicircle area formula is essential for solving a variety of problems in geometry and real-life scenarios. Here are some reasons why this formula is so crucial:
- Practical Applications: From measuring the cross-sectional area of pipes to designing curved furniture, the semicircle area formula has numerous practical uses.
- Foundational Knowledge: It builds a foundation for understanding more advanced geometrical concepts and formulas.
- Problem-Solving: It simplifies the process of calculating areas in complex geometrical shapes that include semicircles.
Without this formula, calculating the area of a semicircular shape would be both time-consuming and less accurate. Thus, mastering the semicircle area formula is not just about solving mathematical problems—it’s about equipping yourself with a versatile tool that has real-world relevance.
How to Derive the Semicircle Area Formula?
Deriving the semicircle area formula is a straightforward process that involves basic geometry and algebra. Here’s how it’s done:
- Start with the Area of a Full Circle: The area of a full circle is given by the formula A = πr², where r is the radius of the circle.
- Divide the Area by Two: Since a semicircle is half of a circle, its area is half of the circle’s area. Therefore, the formula becomes A = (1/2) × πr².
This simple derivation shows how the semicircle area formula is directly related to the area of a full circle, making it both intuitive and easy to remember.
Read also:Amateur Public Naked A Guide To Understanding The Phenomenon
Step-by-Step Guide to Calculating Semicircle Area
Calculating the area of a semicircle involves just a few simple steps. Let’s break it down:
- Identify the Radius: Measure or identify the radius of the semicircle. If you have the diameter, divide it by 2 to get the radius.
- Apply the Formula: Use the formula A = (1/2) × πr² to calculate the area.
- Perform the Calculations: Plug in the value of the radius into the formula and solve for the area. Don’t forget to use the value of π (approximately 3.14159).
By following these steps, you can calculate the area of any semicircle, whether it’s part of a complex geometric shape or a standalone figure.
Semicircle Area Formula with Real-Life Examples
The semicircle area formula is not just a theoretical concept—it has practical applications in various fields. Here are some real-life examples:
- Architecture: Calculating the area of arched windows or doorways.
- Engineering: Measuring the cross-sectional area of pipes and tunnels.
- Design: Creating curved furniture or decorative elements.
These examples highlight the versatility and importance of the semicircle area formula in solving real-world problems.
What Are the Key Variables in the Formula?
The semicircle area formula relies on a few key variables:
- Radius (r): The distance from the center of the circle to any point on its circumference.
- π (Pi): A mathematical constant approximately equal to 3.14159.
Understanding these variables is crucial for correctly applying the formula and avoiding errors in your calculations.
Common Mistakes When Using the Semicircle Area Formula?
Despite its simplicity, there are several common mistakes people make when using the semicircle area formula:
- Forgetting to divide by 2, resulting in the area of a full circle instead of a semicircle.
- Using the diameter instead of the radius in the formula.
- Rounding off π too early in the calculations, leading to less accurate results.
Avoiding these mistakes can save you time and ensure your calculations are accurate.
Semicircle Area in Geometry and Trigonometry
In geometry, the semicircle area formula is used to solve problems involving two-dimensional shapes. In trigonometry, it can be applied to problems involving arcs and sectors. For instance, knowing the area of a semicircle can help in calculating the area of larger, more complex shapes that include semicircular sections.
Applications of the Semicircle Area Formula
The applications of the semicircle area formula are numerous and varied:
- Construction: Designing curved walls, arches, and domes.
- Physics: Calculating the cross-sectional area of curved objects for fluid dynamics.
- Art: Creating geometrically accurate patterns and designs.
These applications underscore the formula’s importance in both academic and professional settings.
How Does the Formula Compare to Other Shapes?
The semicircle area formula is simpler than the formulas for many other shapes, making it an excellent starting point for understanding geometric principles. For example, the formula for the area of a triangle or trapezoid involves more variables and steps, while the semicircle area formula is straightforward and easy to use.
Semicircle Area vs. Full Circle Area
One of the easiest ways to understand the semicircle area formula is by comparing it to the formula for the area of a full circle. Since a semicircle is exactly half of a circle, its area is also half. This relationship makes the semicircle area formula intuitive and easy to remember.
Frequently Asked Questions
1. What is the semicircle area formula?
The semicircle area formula is A = (1/2) × πr², where r is the radius of the semicircle.
2. Can the formula be used for 3D shapes?
No, the formula is specifically for calculating the area of a two-dimensional semicircle.
3. What is the role of π in the formula?
π (Pi) is a constant that represents the ratio of a circle’s circumference to its diameter. It is essential for calculations involving circles and semicircles.
4. How do you find the radius if only the diameter is given?
Simply divide the diameter by 2 to find the radius.
5. Can this formula be applied to irregular semicircles?
No, the formula is only valid for perfect semicircles with uniform radii.
6. Is there a shortcut to memorizing the formula?
Yes! Just remember that it’s half of the area of a full circle: A = (1/2) × πr².
Examples of Semicircle Area in Architecture
From grand arches in ancient Roman buildings to modern-day stadiums, the semicircle area formula plays a crucial role in architecture. Architects use this formula to ensure their designs are both functional and aesthetically pleasing, particularly when working with curved structures.
Conclusion
Mastering the semicircle area formula is an essential step for anyone interested in geometry, mathematics, or related fields. This formula is not only easy to understand but also incredibly versatile, with applications ranging from classroom problems to real-world challenges. By following the steps outlined in this guide, you’ll be well-equipped to calculate semicircle areas accurately and efficiently. So, whether you’re a student, a professional, or just someone curious about geometry, make sure to keep this formula in your mathematical toolkit!