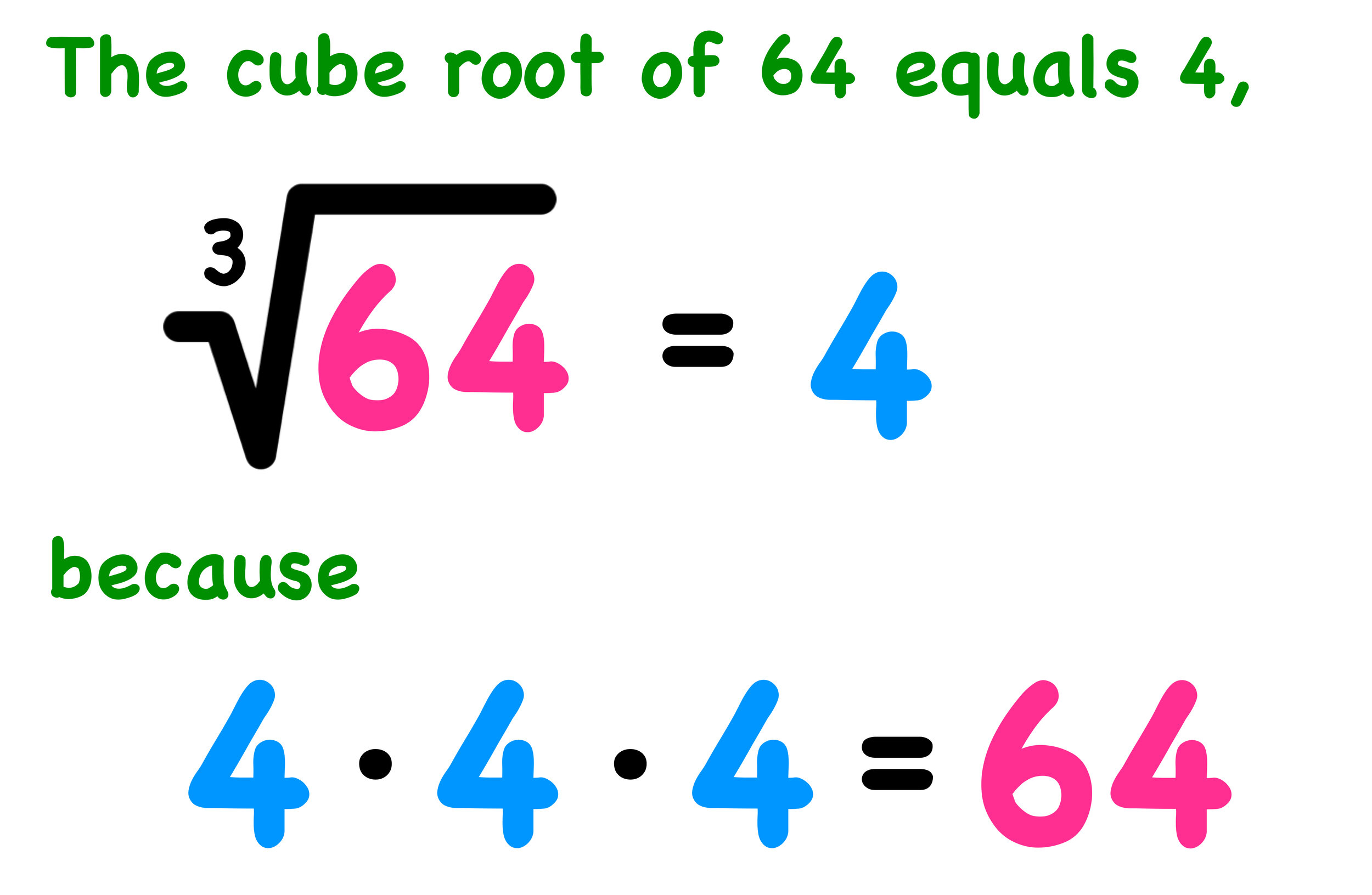The cube root of 512 may seem like a simple mathematical concept, but its implications extend far beyond basic arithmetic. This number holds a special place in mathematics, offering insights into geometry, algebra, and even real-world applications. Understanding the cube root of 512 can unlock a deeper appreciation for mathematical relationships and their importance in everyday life.
At its core, the cube root of 512 answers the question: "What number, when multiplied by itself three times, equals 512?" The answer is 8. While this might sound straightforward, the process of deriving cube roots and grasping their significance can be a fascinating journey through the world of numbers. From ancient civilizations to modern computational methods, cube roots have played an essential role in advancing mathematical knowledge.
But why should we care about the cube root of 512? Beyond its theoretical relevance, this concept finds practical applications in fields like engineering, physics, and computer science. For example, calculating cube roots is vital for determining volumes, processing data, and solving complex equations. In this article, we’ll dive deep into the significance, derivation, and real-world applications of the cube root of 512, peeling back the layers to reveal its true value in mathematics and beyond.
Read also:Experience The Best Mediterranean Cuisine Houston Has To Offer
Table of Contents
- What is the Cube Root of 512?
- How to Calculate the Cube Root of 512?
- Mathematical Properties of Cube Roots
- Why is the Cube Root of 512 Important?
- Geometric Applications of the Cube Root of 512
- Real-World Uses for the Cube Root of 512
- How is the Cube Root of 512 Used in Computer Science?
- Historical Context of Cube Roots
- Common Misunderstandings About the Cube Root of 512
- Step-by-Step Guide to Solving Cube Roots
- Can You Calculate Cube Roots Without a Calculator?
- Fun Facts About the Cube Root of 512
- Frequently Asked Questions
- Conclusion
What is the Cube Root of 512?
The cube root of 512 is the number that, when multiplied by itself three times, equals 512. Mathematically, this can be expressed as:
³√512 = 8
This result means that 8 × 8 × 8 = 512. The cube root is a fundamental concept in mathematics, often introduced in middle or high school and used in advanced studies of algebra and geometry.
In mathematical notation, cube roots are written using the radical (√) symbol with a small "3" above it, indicating the third root. This separates cube roots from square roots, which focus on numbers that, when multiplied by themselves twice, yield the original value.
How to Calculate the Cube Root of 512?
Manual Calculation Method
While the answer to the cube root of 512 is 8, understanding how to calculate it manually can be both educational and satisfying. Here’s a step-by-step breakdown:
- Start with a guess: Since 512 is close to 500, and we know that 8³ = 512, you can start by guessing 8.
- Refine the guess: Use division to confirm your guess. Divide 512 by 8 twice to check if the product equals 8.
- Verify the result: Multiply your result three times to ensure it equals 512.
Using a Calculator
Most scientific calculators offer a cube root function. Simply input "512" and press the cube root button to get the result. This method is quicker and more accurate, especially for less straightforward numbers.
Read also:Super Mario Brothers The Iconic Legacy Of Gamings Most Famous Plumbers
Mathematical Properties of Cube Roots
Cube roots share several fascinating mathematical properties that make them valuable in many areas of study:
- Non-Negative Outputs: The cube root of any non-negative number is also non-negative.
- Unique Solutions: Unlike square roots, cube roots have only one real solution.
- Inverse Relationship: Cube roots are the inverse operation of raising a number to the power of three.
These properties make cube roots crucial in solving equations, modeling physical phenomena, and analyzing data.
Why is the Cube Root of 512 Important?
Understanding the cube root of 512 is not just an academic exercise—it has real-world significance. Here’s why it matters:
- Volume Calculations: Cube roots are essential for determining the dimensions of cubic structures.
- Physics and Engineering: Many formulas in physics and engineering rely on cube root calculations.
- Data Science: Cube roots help process and normalize large datasets in computational fields.
Geometric Applications of the Cube Root of 512
In geometry, the cube root of a number often helps calculate the side length of a cube given its volume. For example, if a cube’s volume is 512 cubic units, its side length will be 8 units. This relationship is invaluable in architecture, engineering, and design.
Real-World Uses for the Cube Root of 512
The cube root of 512 finds applications in various real-world scenarios, including:
- Material Science: Calculating densities and volumes.
- Architecture: Designing cubic structures and spaces.
- Technology: Optimizing data storage and processing.
How is the Cube Root of 512 Used in Computer Science?
In computer science, cube roots are used for algorithms, data processing, and 3D modeling. Calculations involving cube roots are foundational in machine learning, graphics rendering, and computational geometry.
Historical Context of Cube Roots
Cube roots have been studied for centuries, dating back to ancient Greek and Indian mathematicians. Their methods for finding cube roots laid the groundwork for modern mathematical techniques.
Common Misunderstandings About the Cube Root of 512
Some misconceptions about cube roots include:
- They are the same as square roots (false).
- They apply only to whole numbers (false).
- They have multiple real solutions (false).
Step-by-Step Guide to Solving Cube Roots
Follow this guide to find cube roots manually:
- Estimate the root based on nearby perfect cubes.
- Use division and refinement to hone your guess.
- Verify your solution by cubing it.
Can You Calculate Cube Roots Without a Calculator?
Yes! Although it takes practice, manual methods and estimation can help solve cube roots without a calculator.
Fun Facts About the Cube Root of 512
- The cube root of 512 is a whole number, making it unique among cube roots.
- It’s often used in educational examples due to its simplicity.
Frequently Asked Questions
1. What is the cube root of 512?
The cube root of 512 is 8.
2. How do you manually find the cube root of 512?
You can use estimation, division, and verification to calculate it manually.
3. Is the cube root of 512 a whole number?
Yes, it is a whole number: 8.
4. Why is the cube root of 512 significant?
It has applications in geometry, engineering, and computer science.
5. Can I use the cube root of 512 in real life?
Absolutely! It’s used in volume calculations and data analysis.
6. What are some related concepts to the cube root of 512?
Square roots, exponents, and logarithms are closely related concepts.
Conclusion
The cube root of 512 is more than just an answer to a mathematical question—it’s a gateway to understanding deeper principles of mathematics and their applications. From its role in geometry to its importance in computer science, this seemingly simple calculation offers profound insights and practical uses. Whether you’re a student, a professional, or just curious about numbers, exploring the cube root of 512 can enrich your understanding of the mathematical world.