The process of integrating inverse trigonometric functions, such as the inverse tangent (arctan), plays a crucial role in calculus and advanced mathematics. Known for its diverse applications in engineering, physics, and computer science, the integration of inverse tan is a topic that requires both precision and a solid understanding of foundational principles. Whether solving complex integrals or applying the concept to real-world problems, mastering this topic is essential for learners and professionals alike.
At its core, the integral of the inverse tan function provides a bridge between theoretical math and practical solutions. It helps evaluate areas under curves, solve differential equations, and even model certain natural phenomena. For students and enthusiasts delving into calculus, understanding how to integrate inverse tan not only builds confidence but also paves the way for tackling more advanced mathematical challenges.
This comprehensive guide is designed to simplify the topic of integrating inverse tan. With clear explanations, step-by-step procedures, and practical examples, this article will equip you with the tools to confidently approach this integral. So, if you're ready to enhance your mathematical toolkit and gain deeper insights into calculus, let’s dive into the intricacies of integrating inverse tan.
Read also:All About Caden Tellier A Rising Star In The World Of Sports
Table of Contents
- What is Inverse Tan?
- Why is Integrating Inverse Tan Important?
- How Do You Integrate Inverse Tan?
- Step-by-Step Integration of Inverse Tan
- Applications of Integrating Inverse Tan
- Common Mistakes to Avoid
- Is Inverse Tan Related to Other Trigonometric Functions?
- Real-World Examples of Inverse Tan Integration
- What Are Some Useful Tips for Simplifying Integrals?
- Inverse Tan in Higher Mathematics
- Differences Between Arctan and Other Inverse Functions
- How Does the Integral of Inverse Tan Differ from Its Derivative?
- Frequently Asked Questions
- Conclusion
What is Inverse Tan?
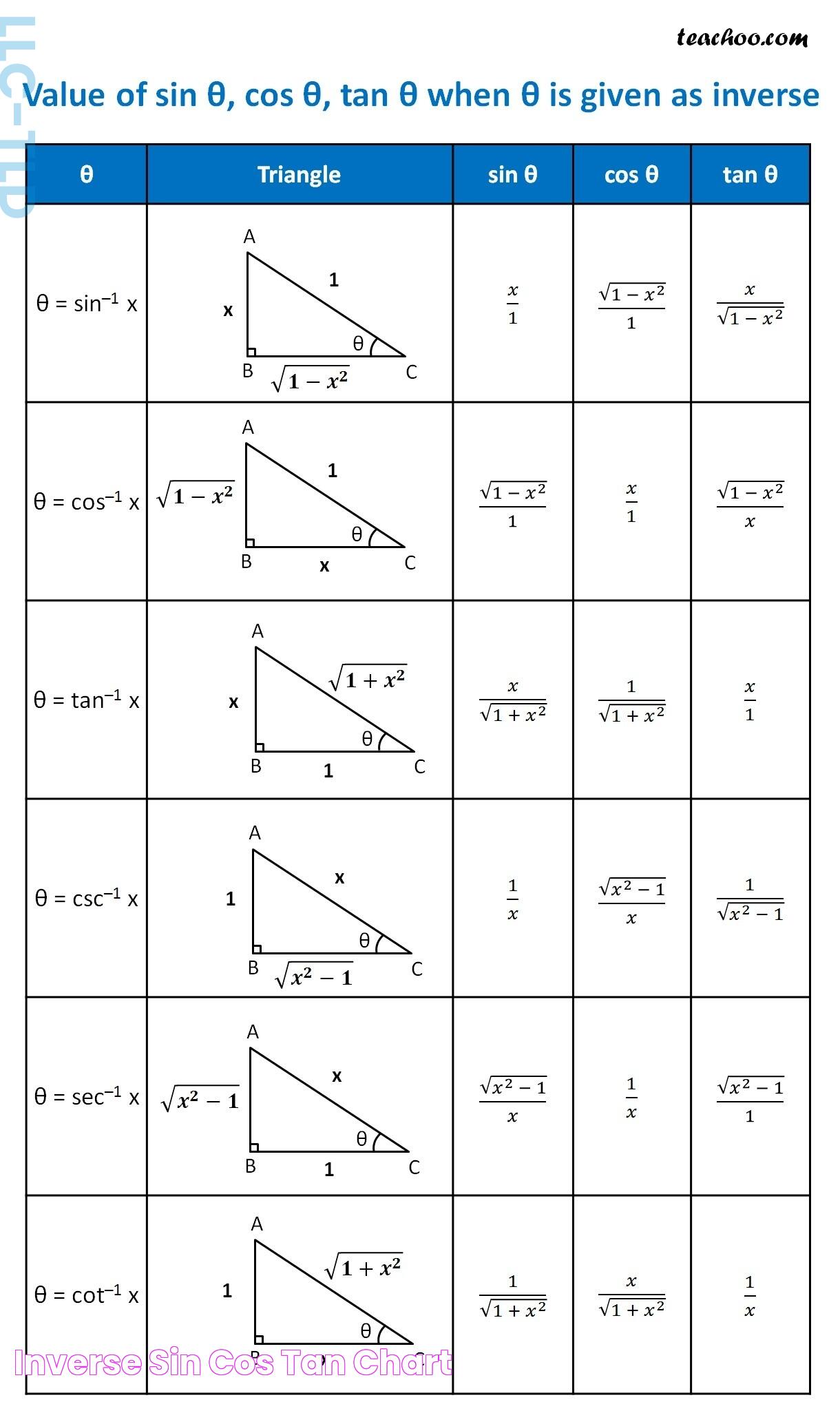
The inverse tangent function, commonly written as arctan(x) or tan-1(x), is the inverse of the tangent function in trigonometry. In simpler terms, it reverses the operation of the tangent function. If y = tan(x), then x = arctan(y). The function is defined over a specific range to ensure it is one-to-one and thus invertible. For arctan(x), the usual range is [-π/2, π/2].
Graphically, the inverse tangent function is a curve that gradually increases but never exceeds π/2 or falls below -π/2. It is continuous and has a horizontal asymptote at these values, making it a crucial function in both theoretical and applied mathematics.
Key Properties of Inverse Tan
- Domain: All real numbers (-∞, ∞)
- Range: [-π/2, π/2]
- Derivative: d/dx [arctan(x)] = 1 / (1 + x2)
Understanding these properties is essential when approaching the integration of arctan(x), as they form the basis for solving complex integrals involving this function.
Why is Integrating Inverse Tan Important?
The integration of inverse tan is significant because it frequently appears in problems involving areas, volumes, and other geometric calculations. Its applications span across various fields, including:
- Engineering: Used in signal processing and systems design.
- Physics: Integral to understanding motion and forces.
- Computer Science: Plays a role in algorithms and machine learning.
Moreover, the integral of inverse tan provides a foundation for solving other trigonometric integrals, making it a versatile tool in calculus.
How Do You Integrate Inverse Tan?
Integrating the inverse tangent involves applying specific techniques to simplify the process. The standard formula for integrating arctan(x) is:
Read also:Heart Break Healing And Growth Beyond The Pain
∫ arctan(x) dx = x * arctan(x) - 1/2 * ln(1 + x2) + C
Key Steps for Integration
- Identify the integral involving arctan(x).
- Apply the formula or use integration by parts if necessary.
- Simplify the result and include the constant of integration (C).
Each of these steps will be elaborated upon in the following sections, with examples to illustrate the application of the formula.
Step-by-Step Integration of Inverse Tan
To integrate arctan(x), let us break the process down into manageable steps using the formula provided earlier:
Example Problem
Find the integral of arctan(x) with respect to x.
Solution:
- Write down the integral: ∫ arctan(x) dx
- Use the formula: x * arctan(x) - 1/2 * ln(1 + x2) + C
- Substitute and simplify: The result is x * arctan(x) - 1/2 * ln(1 + x2) + C
This is the general solution for the integral of arctan(x). For definite integrals, the process involves substituting the limits into the solution obtained.
Applications of Integrating Inverse Tan
The integral of inverse tan has diverse applications. Some notable examples include:
- Calculating Areas: Used to find the area under curves defined by trigonometric functions.
- Physics Problems: Appears in problems involving angular motion and periodic systems.
- Engineering: Integral for solving equations in control systems and signal analysis.
These applications highlight the importance of understanding the integration of inverse tan in both academic and professional contexts.
Common Mistakes to Avoid
When integrating inverse tan, learners often make errors that can lead to incorrect results. Here are some common pitfalls and how to avoid them:
- Forgetting the Constant of Integration: Always include "+ C" in indefinite integrals.
- Misapplying the Formula: Ensure the correct formula is used for arctan(x).
- Ignoring Simplifications: Simplify logarithmic and trigonometric terms to avoid complex expressions.
By paying attention to these details, you can minimize errors and achieve accurate results.
Is Inverse Tan Related to Other Trigonometric Functions?
Yes, inverse tan is closely related to other trigonometric functions. It forms part of the family of inverse trigonometric functions, which includes arcsin(x) and arccos(x). These functions are interconnected and often appear together in complex integrals and equations.
For instance, the derivative of arctan(x) involves the expression 1/(1 + x2), which is also present in some integrals of arcsin(x) and arccos(x). Understanding these relationships can simplify calculations and enhance problem-solving abilities.
Real-World Examples of Inverse Tan Integration
Integrating inverse tan is not just a theoretical exercise; it has practical applications in various fields:
- Traffic Engineering: Used to model vehicle acceleration and deceleration curves.
- Economics: Appears in certain growth models and optimization problems.
- Medicine: Helps in imaging techniques like MRI and CT scans.
These examples demonstrate the versatility of inverse tan integration and its relevance to real-world problems.
What Are Some Useful Tips for Simplifying Integrals?
Simplifying integrals involving inverse tan can be challenging, but the following tips can make the process easier:
- Substitution: Use substitution to simplify complicated expressions.
- Integration by Parts: Apply this technique when the integral involves a product of functions.
- Review Trigonometric Identities: Familiarity with these identities can simplify calculations.
With these tips, you can approach integrals more confidently and efficiently.
Inverse Tan in Higher Mathematics
In higher mathematics, inverse tan plays a crucial role in topics such as Fourier analysis, Laplace transforms, and differential equations. Its properties and integrals are foundational in these advanced areas, making it a topic worth mastering for students pursuing higher studies in mathematics and related fields.
Differences Between Arctan and Other Inverse Functions
While arctan(x), arcsin(x), and arccos(x) are all inverse trigonometric functions, they differ in terms of their domains, ranges, and applications. For example:
- Arctan(x): Domain is all real numbers, range is [-π/2, π/2].
- Arcsin(x): Domain is [-1, 1], range is [-π/2, π/2].
- Arccos(x): Domain is [-1, 1], range is [0, π].
Understanding these differences is essential for correctly solving integrals and equations involving these functions.
How Does the Integral of Inverse Tan Differ from Its Derivative?
The integral of inverse tan and its derivative serve different purposes in calculus:
- Derivative: Represents the rate of change of the function and is given by 1/(1 + x2).
- Integral: Represents the area under the curve of arctan(x) and is expressed as x * arctan(x) - 1/2 * ln(1 + x2) + C.
While the derivative focuses on instantaneous change, the integral provides a cumulative measure, highlighting their complementary nature in calculus.
Frequently Asked Questions
What is the formula for integrating inverse tan?
The formula is ∫ arctan(x) dx = x * arctan(x) - 1/2 * ln(1 + x2) + C.
Can I use substitution for integrating arctan(x)?
Yes, substitution is a helpful technique, especially when the integral involves more complex expressions.
What are some real-world applications of inverse tan integration?
Applications include physics (motion analysis), engineering (signal processing), and economics (growth models).
Is arctan(x) the same as tan-1(x)?
Yes, arctan(x) and tan-1(x) are two notations for the same function.
How is the integral of arctan(x) used in engineering?
It is used in systems design, control theory, and analyzing angular motion in engineering applications.
Why is the constant of integration important?
The constant of integration accounts for all possible solutions of an indefinite integral and ensures mathematical accuracy.
Conclusion
Integrating inverse tan is a vital skill in calculus, with applications that extend far beyond the classroom. By understanding the properties of arctan(x), applying the formula accurately, and avoiding common mistakes, you can master this topic and unlock its potential in various fields. Whether you're a student, engineer, or scientist, the tools and insights provided in this guide will serve as a solid foundation for tackling complex mathematical challenges. So, keep practicing, and you'll soon find integrating inverse tan to be second nature!